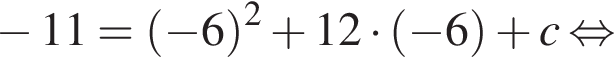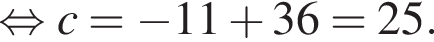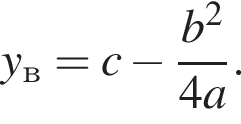1. Задание № 1054 

Сложность: IV
Классификатор стереометрии: 3\.10\. Правильная треугольная призма, 3\.18\. Шар, 3\.21\. Комбинации многогранников и круглых тел, 4\.1\. Площадь поверхности многогранников
Площади
i
Найдите площадь полной поверхности прямой треугольной призмы, описанной около шара, если площадь основания призмы равна 7,5.
Решение. Поскольку шар вписан в призму, то окружность большого круга шара вписывается в основание призмы, т. е. в треугольник. Исходя из этого, площадь основания призмы равна 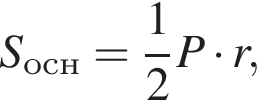 где P — периметр основания призмы, r — радиус шара. Кроме того, высота призмы равна диаметру шара, т. е.
где P — периметр основания призмы, r — радиус шара. Кроме того, высота призмы равна диаметру шара, т. е. 
Площадь полной поверхности прямой треугольной призмы равна (a, b, c — стороны основания призмы):
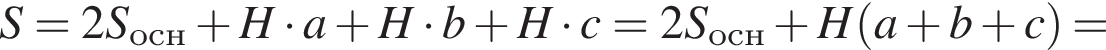
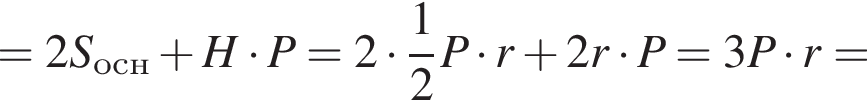

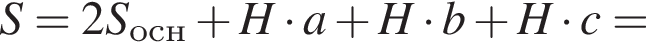
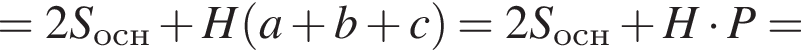
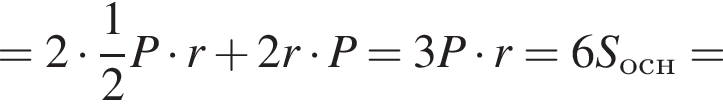

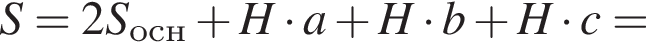

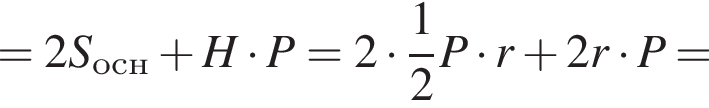


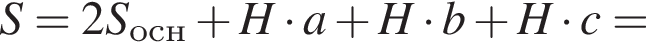


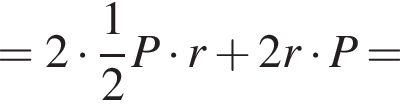


![]()



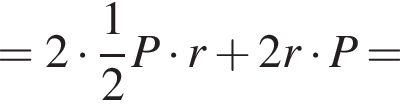


Ответ: 45.
Ответ: 45
1054
45
Сложность: IV
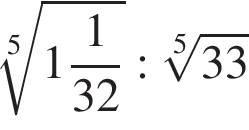 равно:
равно: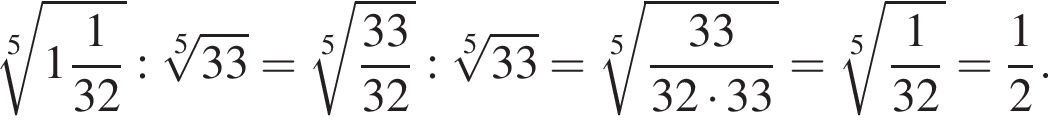
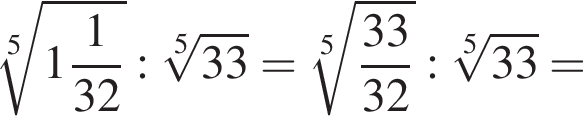
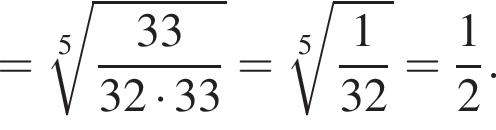

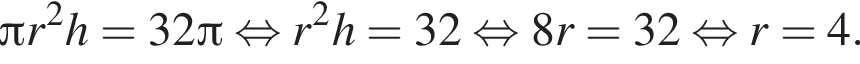

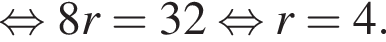
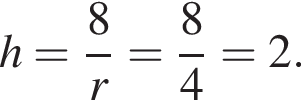
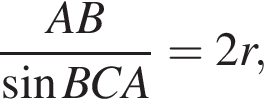 откуда
откуда 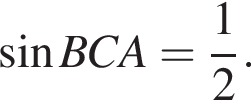 Из прямоугольного треугольника BHC имеем:
Из прямоугольного треугольника BHC имеем: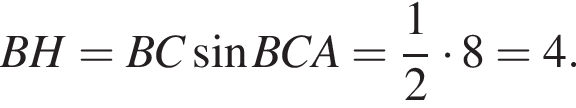
 то значение α с точностью до сотых равно:
то значение α с точностью до сотых равно: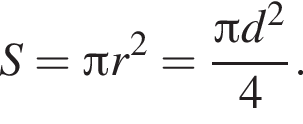 Следовательно,
Следовательно, 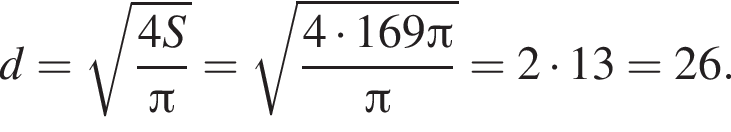
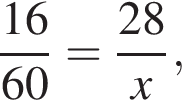 где x — неизвестное число.
где x — неизвестное число.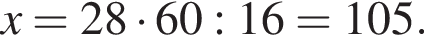
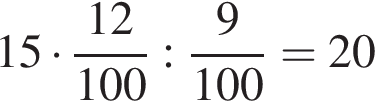 л.
л.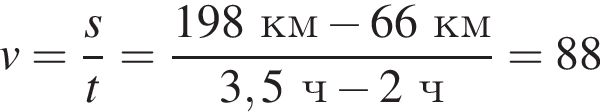 км/ч.
км/ч.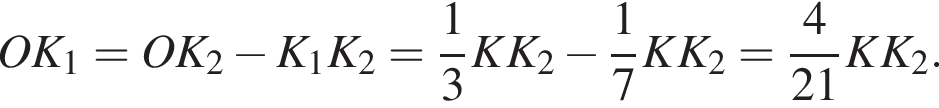
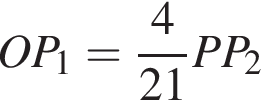 и
и 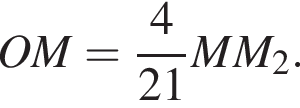
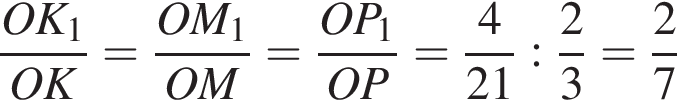 и треугольники M1K1P1 и MKP подобны, получаем
и треугольники M1K1P1 и MKP подобны, получаем 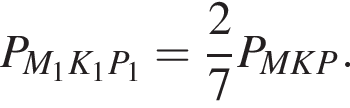 Тогда
Тогда 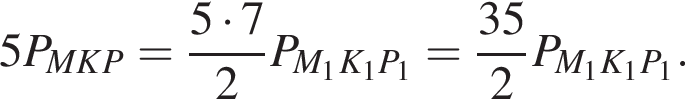 Тогда точка B обойдет периметр 70 раз.
Тогда точка B обойдет периметр 70 раз.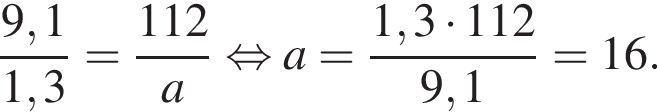
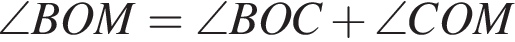 и
и  Таким образом:
Таким образом:
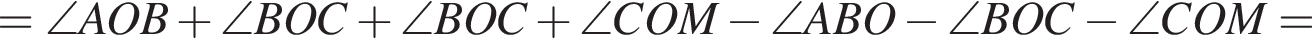
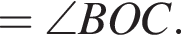

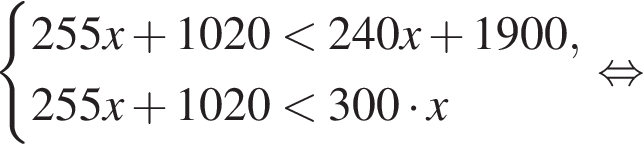
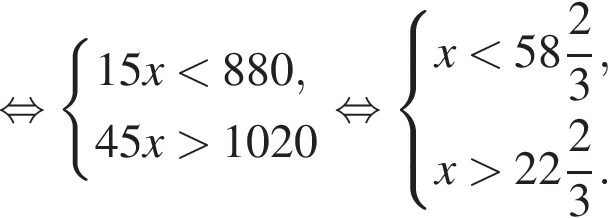
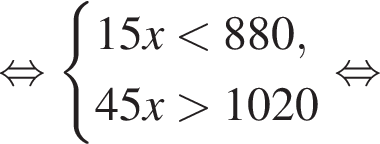
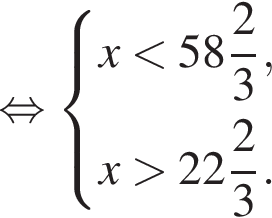
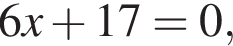 то
то  равно:
равно: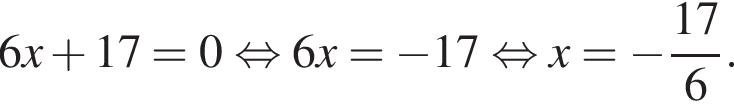
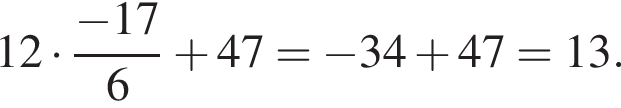
 поэтому
поэтому 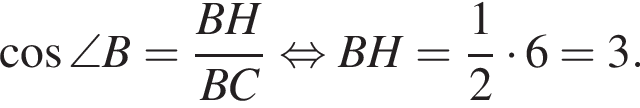 Следовательно,
Следовательно, 
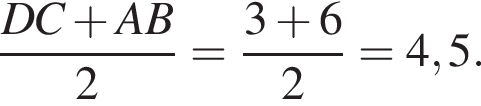
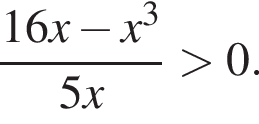
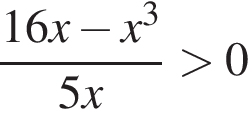
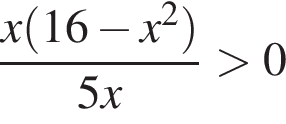
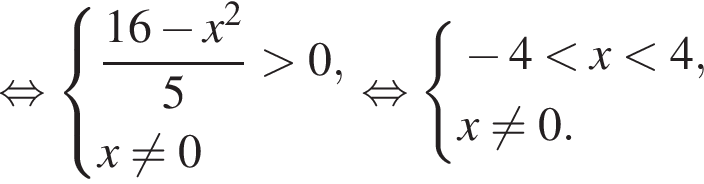
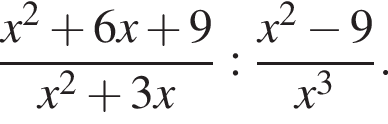
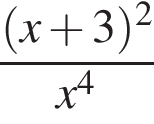
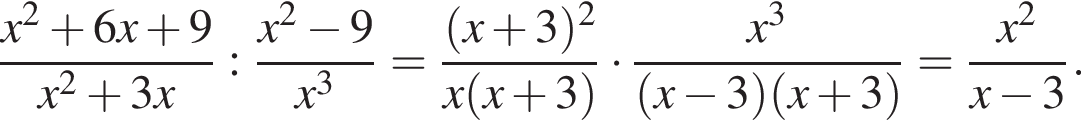
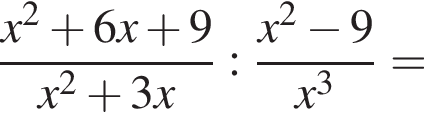
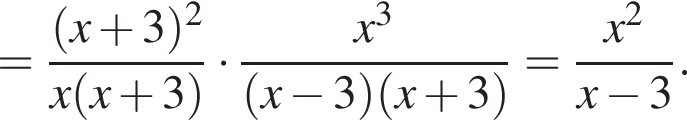
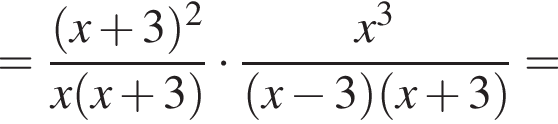
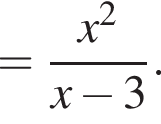
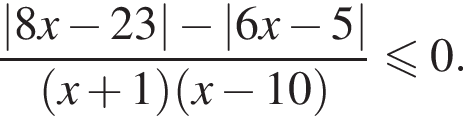
 совпадает со знаком разности
совпадает со знаком разности  имеем:
имеем: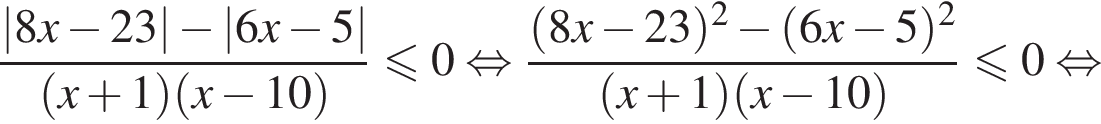
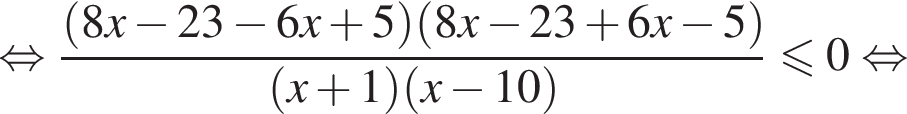
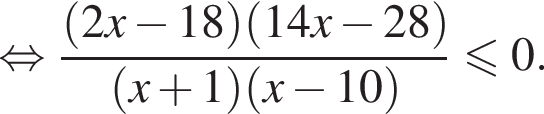
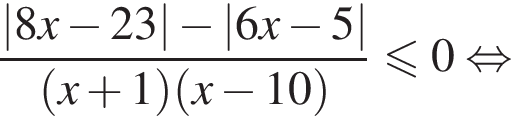
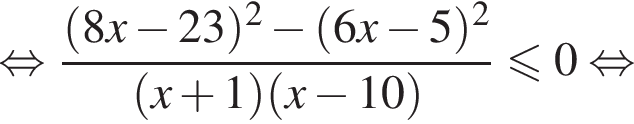
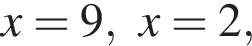 корни знаменателя
корни знаменателя 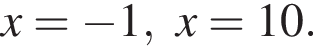 Поэтому:
Поэтому: 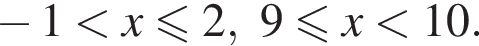 Целые решения — числа 0, 1, 2, 9. Их сумма равна 12.
Целые решения — числа 0, 1, 2, 9. Их сумма равна 12.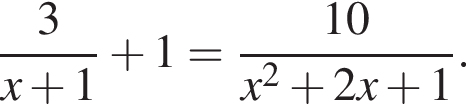
 :
: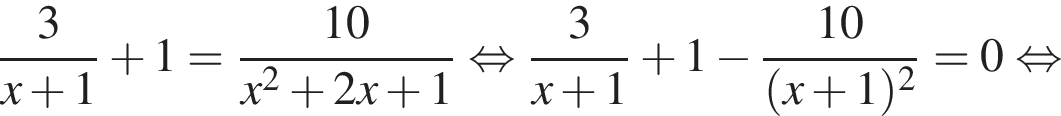
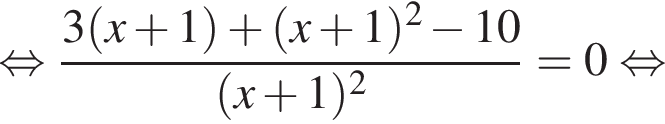
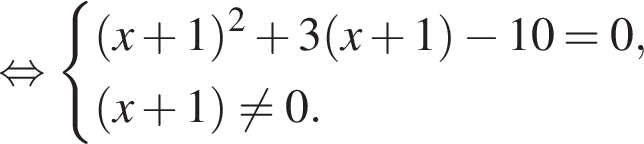
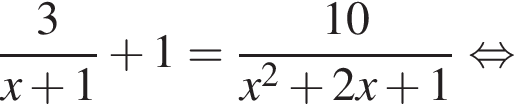
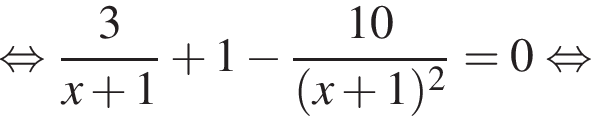
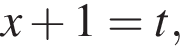 тогда:
тогда: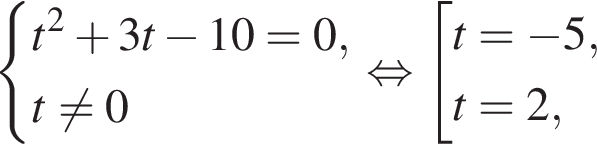
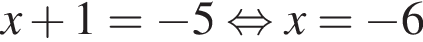 или
или 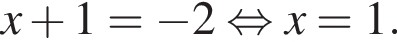

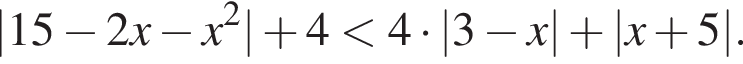
 имеем:
имеем: 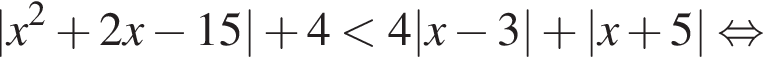
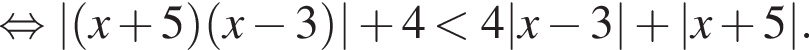
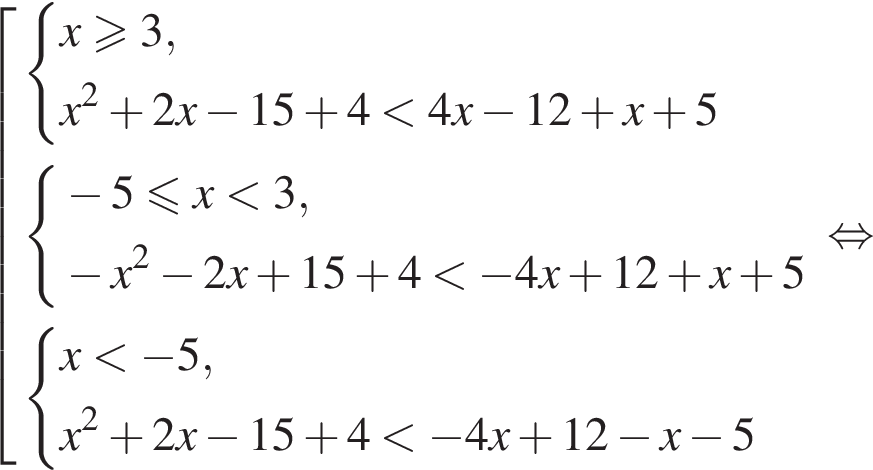
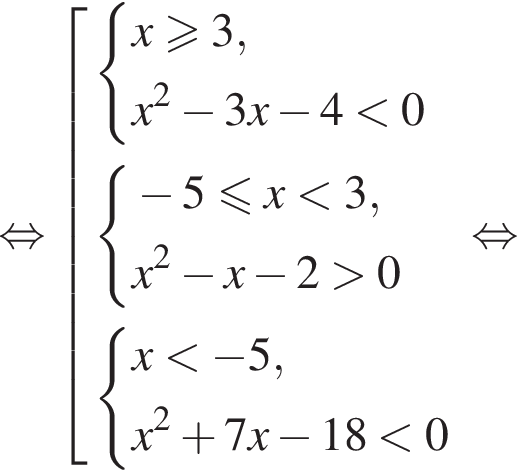
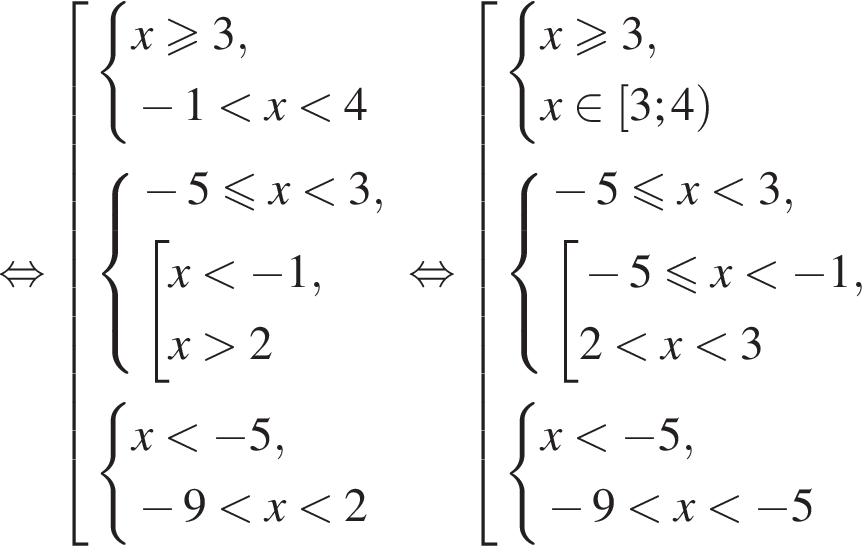
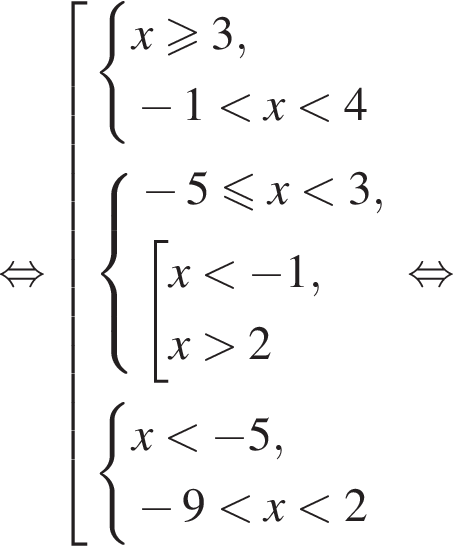
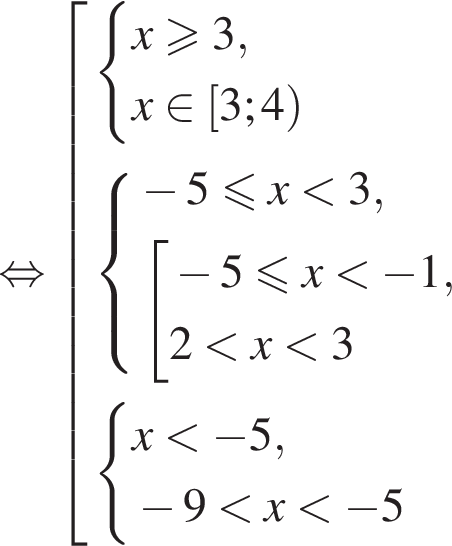
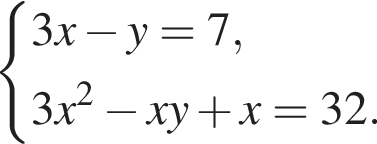

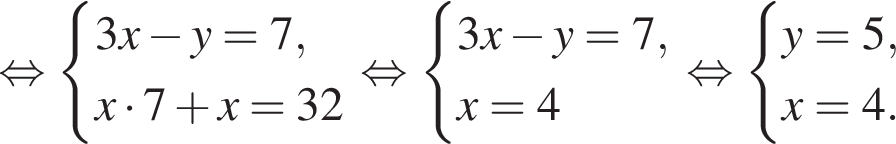
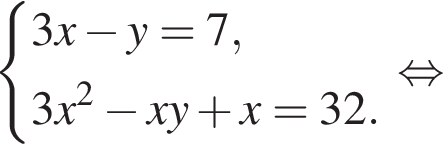
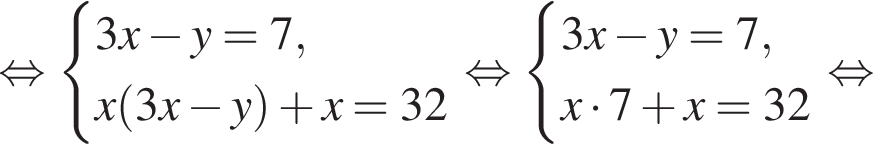
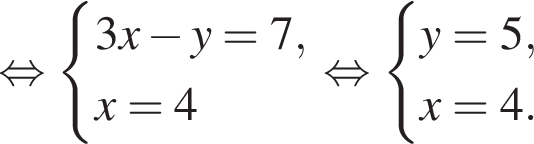
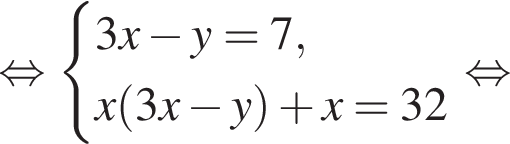
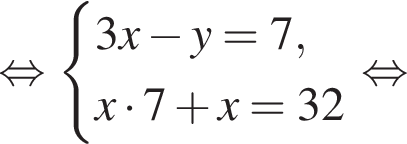
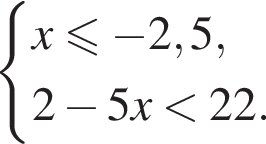
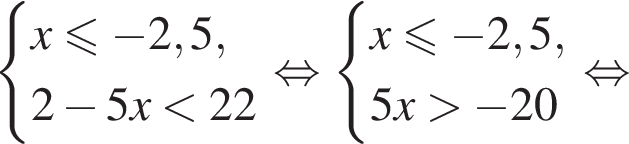
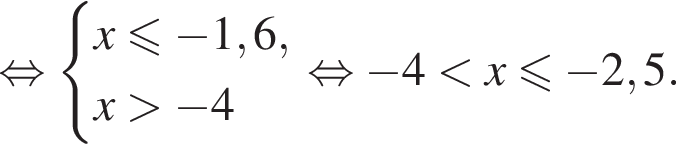
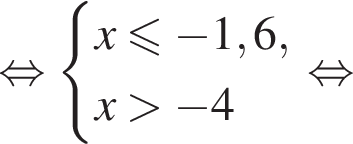
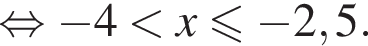
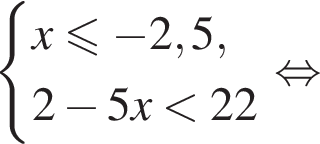
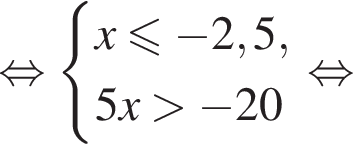
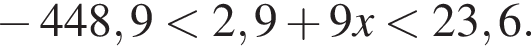
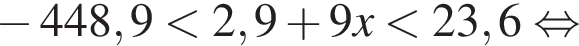
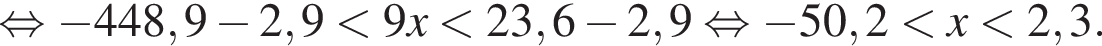

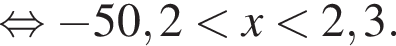
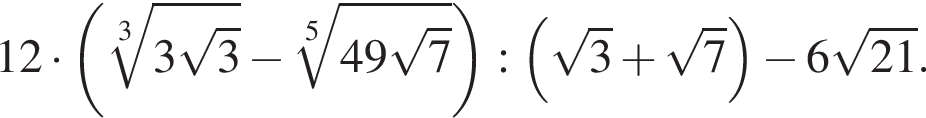
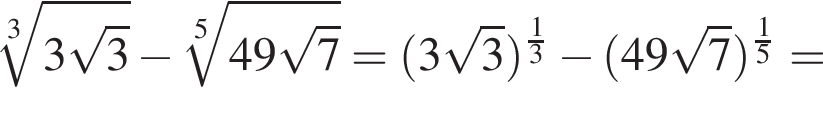
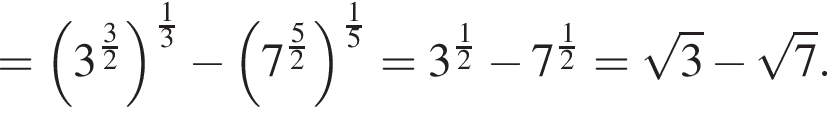
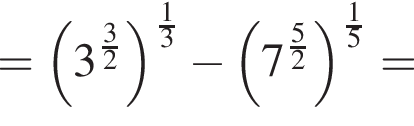
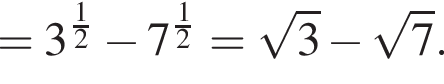
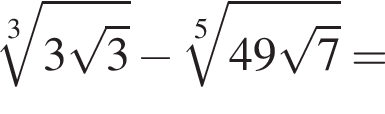
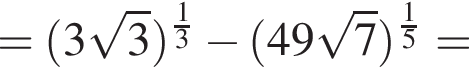
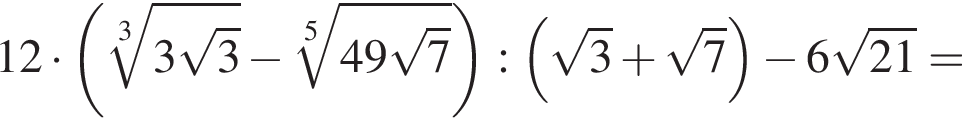
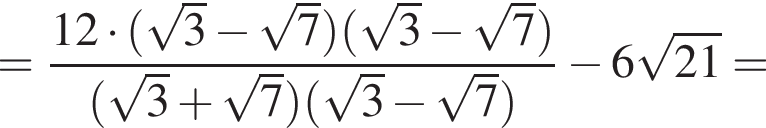
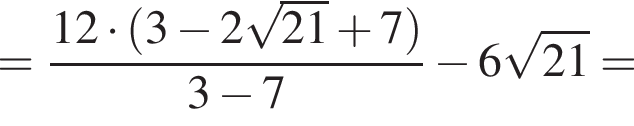
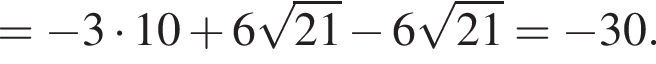

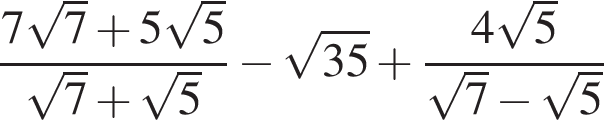
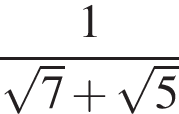
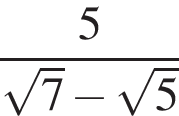
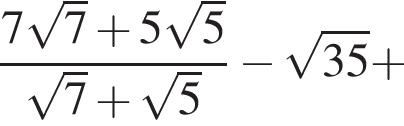
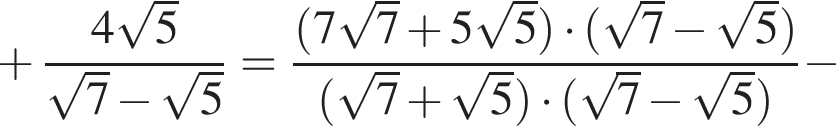
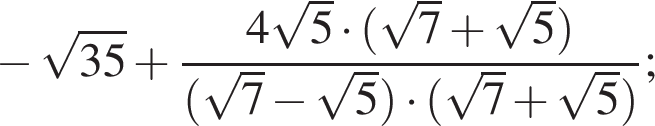

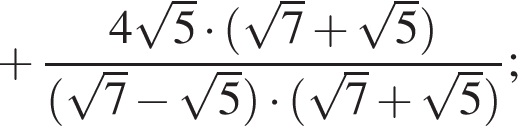
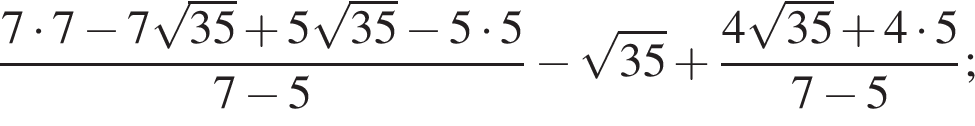
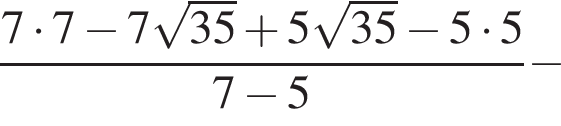
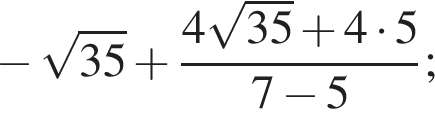
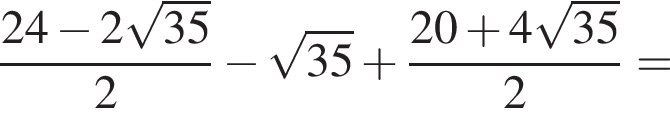
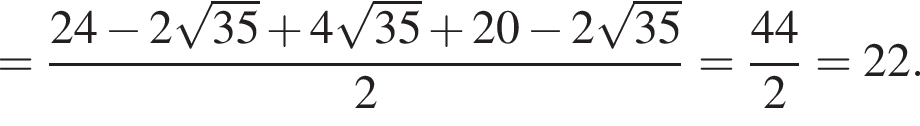
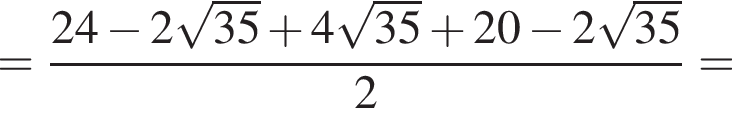
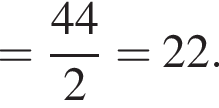
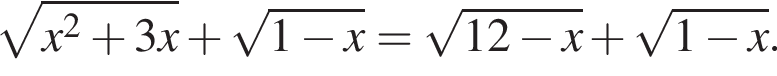
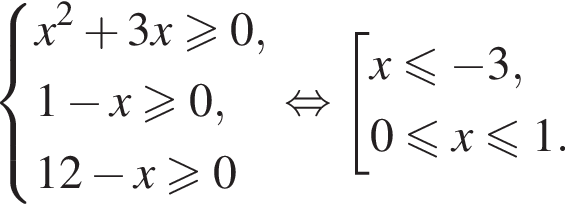
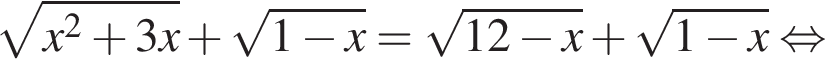
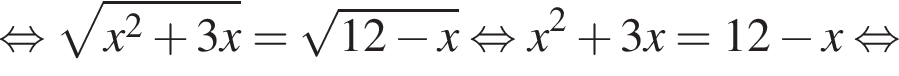
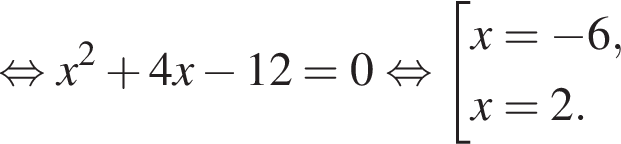
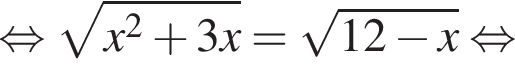
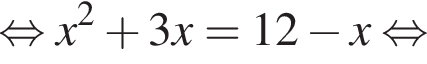
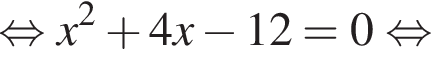
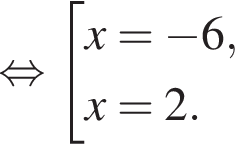

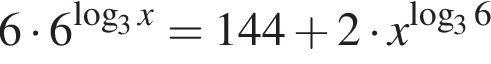 равна ...
равна ...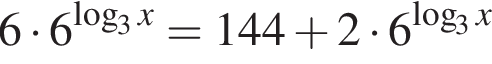
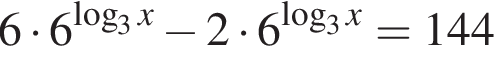
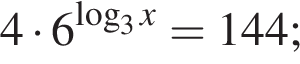
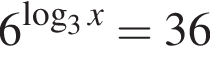
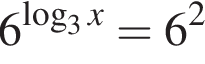
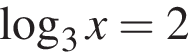
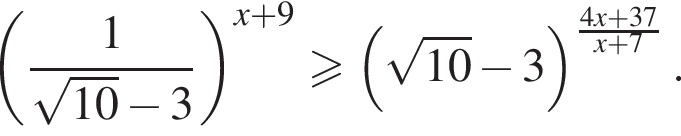 В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −5].
В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −5].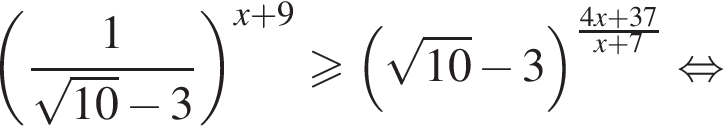
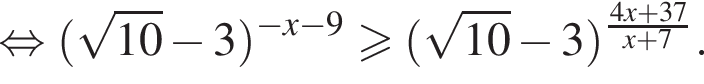
 неравенство будет выполняться при
неравенство будет выполняться при 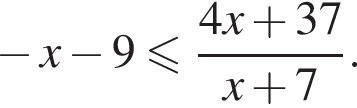 Имеем:
Имеем: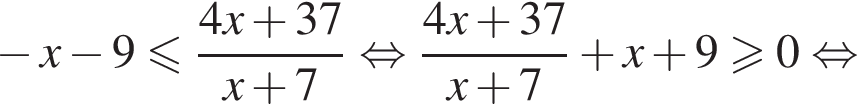
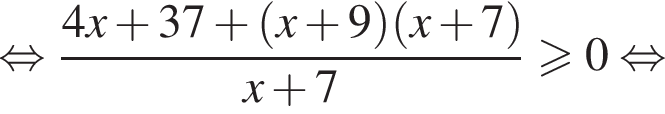
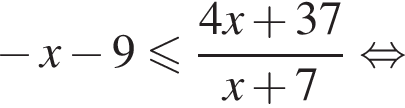
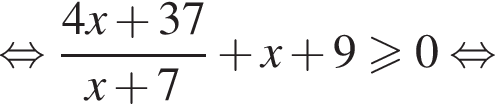
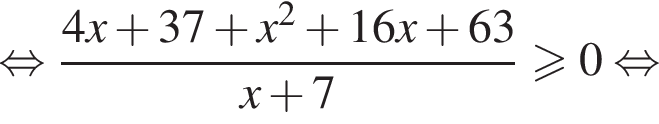
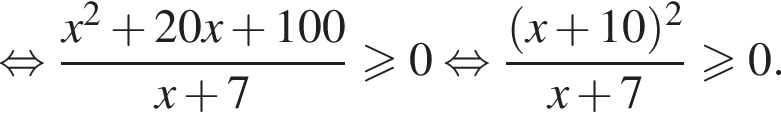
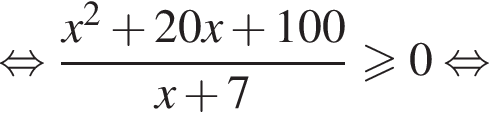
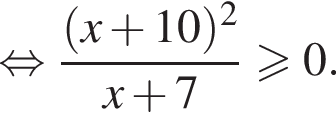
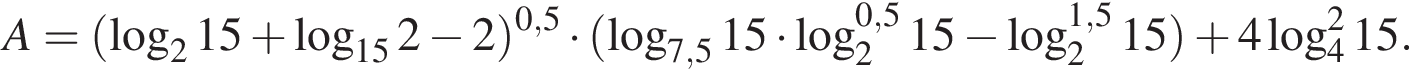

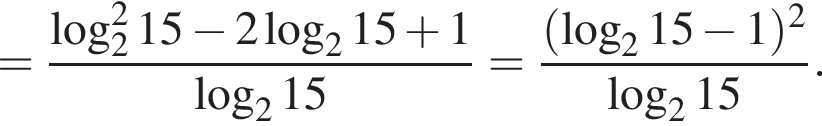
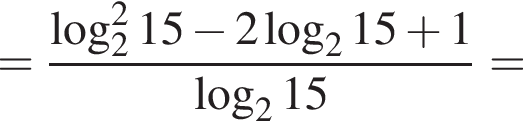
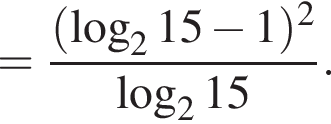
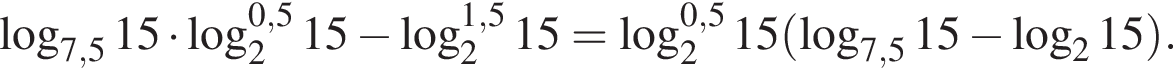
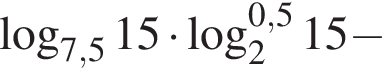
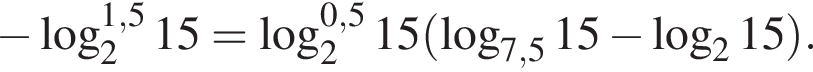
 Тогда имеем:
Тогда имеем: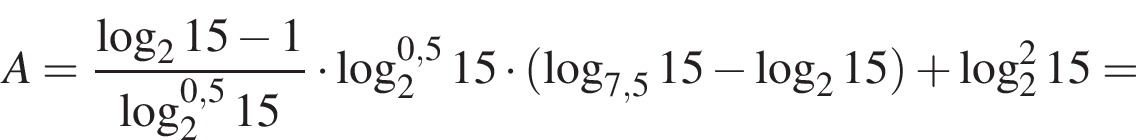
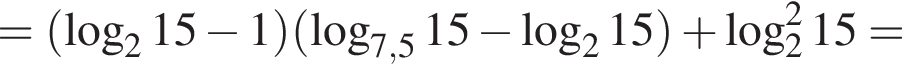
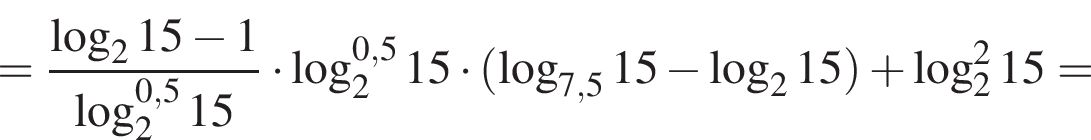
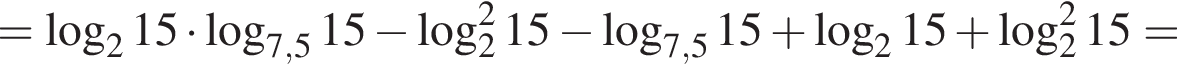
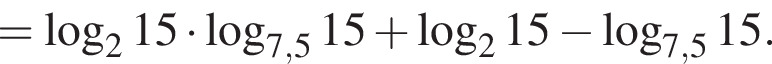
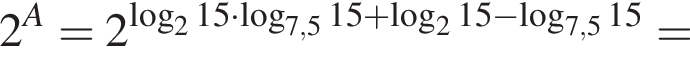
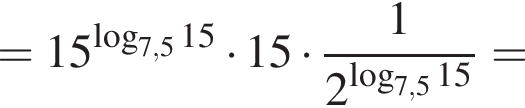
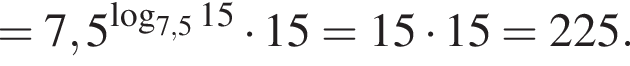
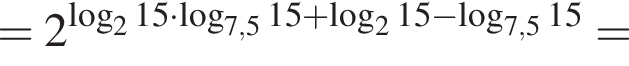
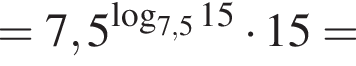
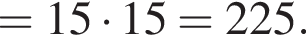
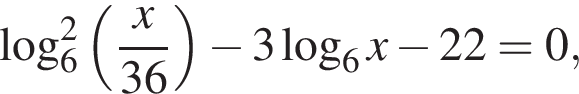 тогда значение выражения
тогда значение выражения 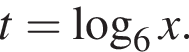
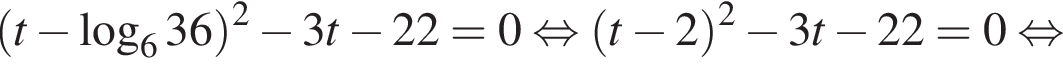
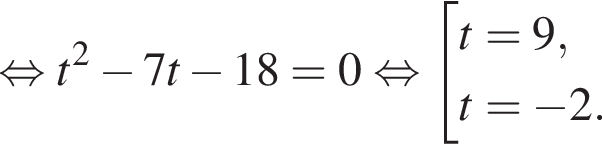
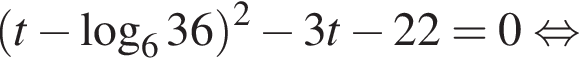
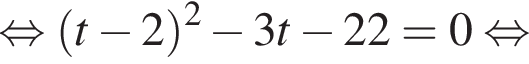
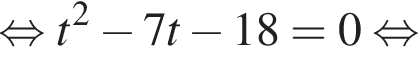
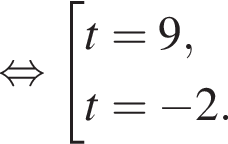
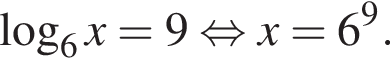 Тогда
Тогда 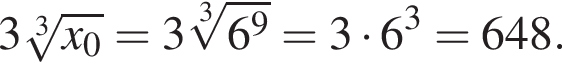
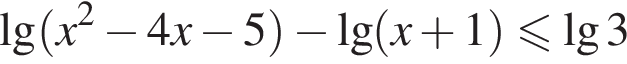 равно:
равно: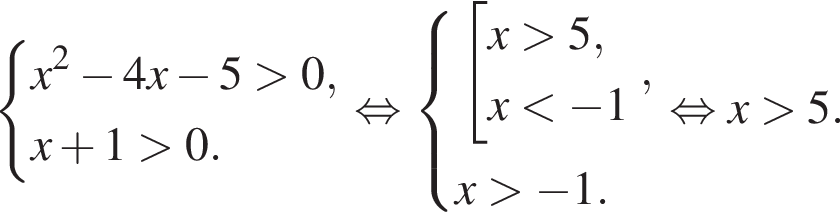
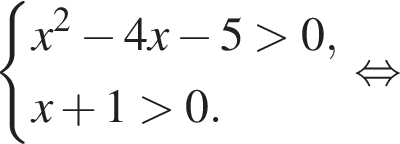
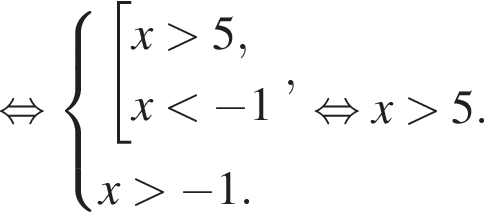
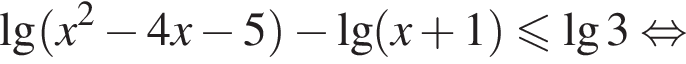
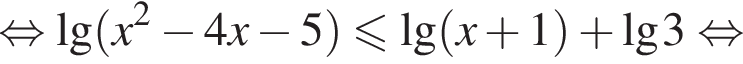
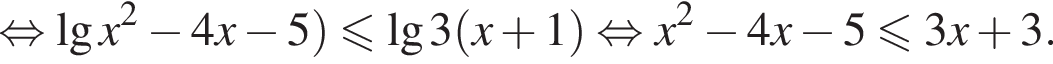
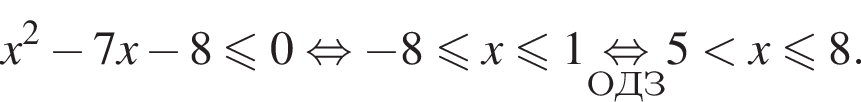
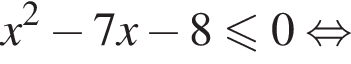
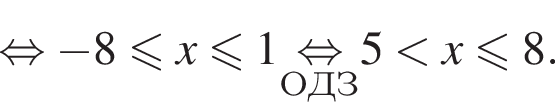
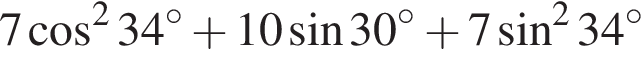 равно:
равно: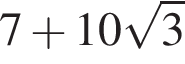
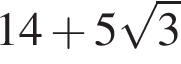

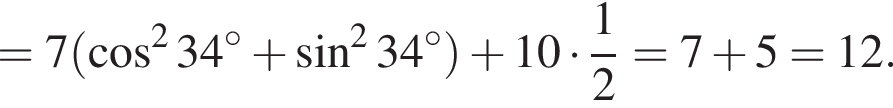
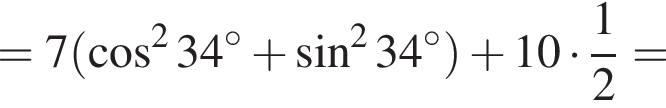
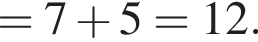
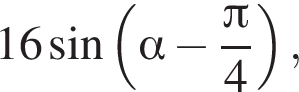 если
если 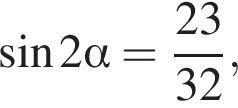
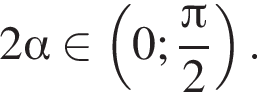
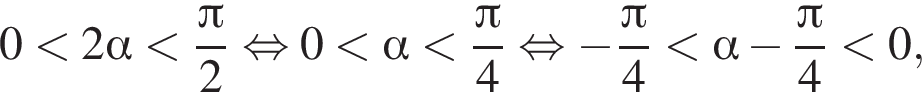

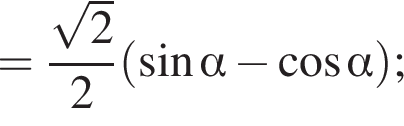
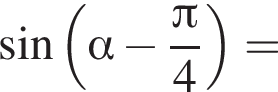
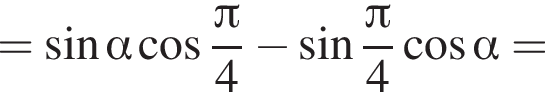
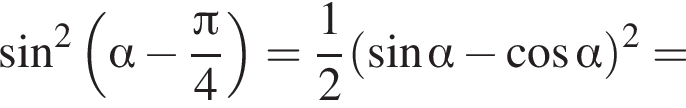
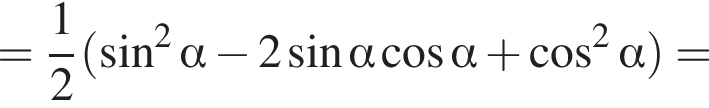
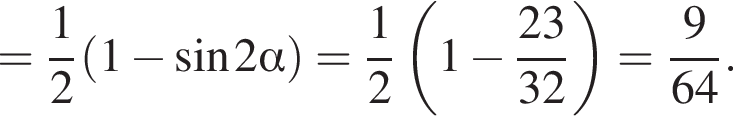
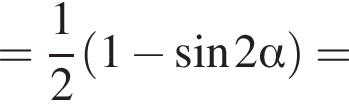
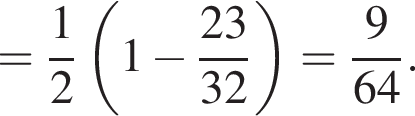
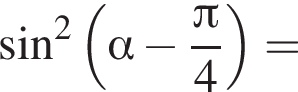
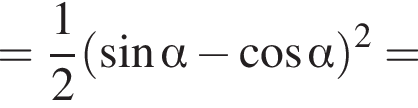
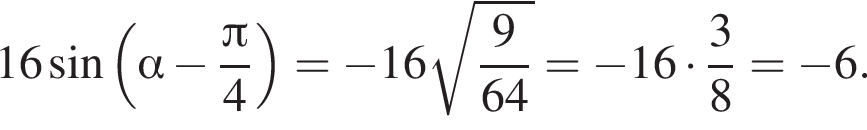
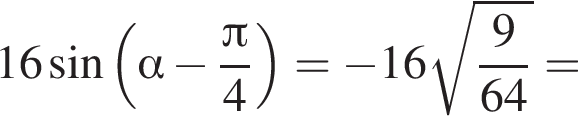
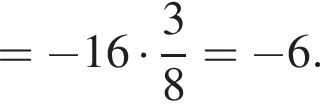
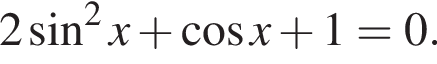
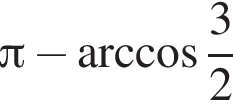
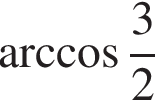
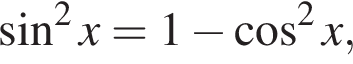 получим:
получим: 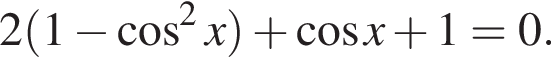 Сделаем замену
Сделаем замену 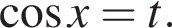 Решим уравнение:
Решим уравнение:
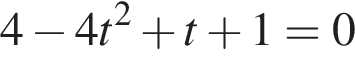
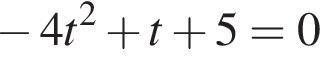
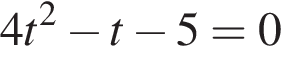
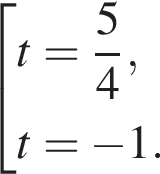
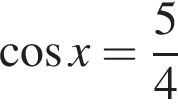 или
или 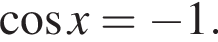 Первое уравнение решений не имеет, поскольку
Первое уравнение решений не имеет, поскольку 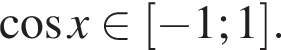 Рассмотрим второе уравнение:
Рассмотрим второе уравнение: 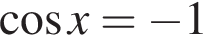
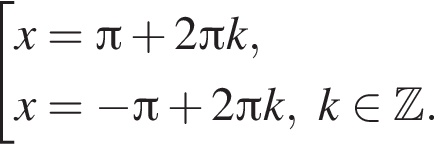
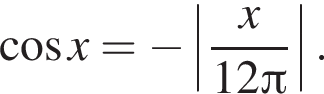

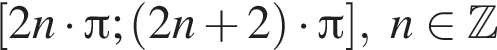 вплоть до
вплоть до 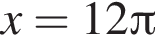 решений нет. Поэтому на положительной полуоси уравнение имеет 12 решений. В силу четности левой и правой частей уравнения всего имеем 24 решения.
решений нет. Поэтому на положительной полуоси уравнение имеет 12 решений. В силу четности левой и правой частей уравнения всего имеем 24 решения.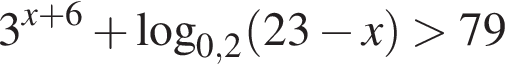 равно ...
равно ...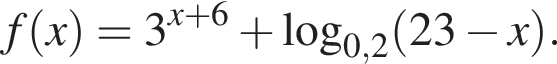 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 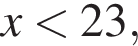 и что на
и что на 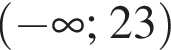
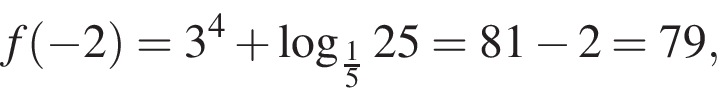 неравенство верно для всех x из
неравенство верно для всех x из 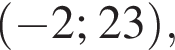 который содержит 24 целых числа.
который содержит 24 целых числа.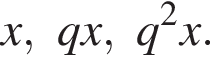
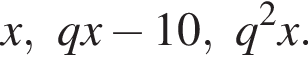
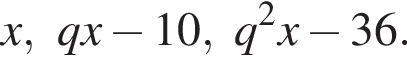
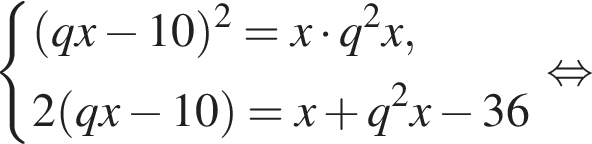
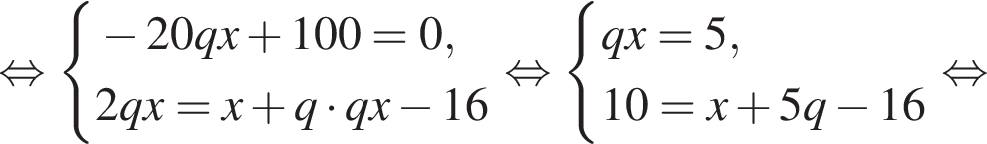
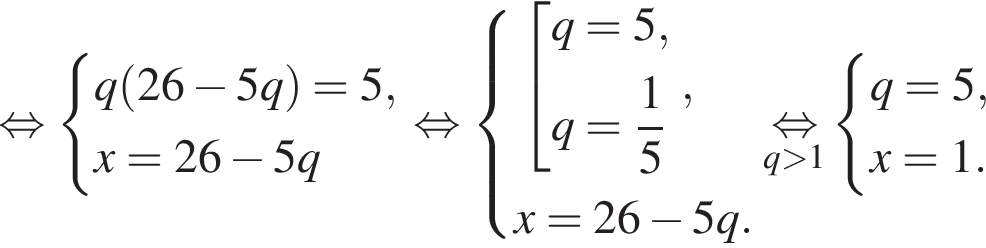
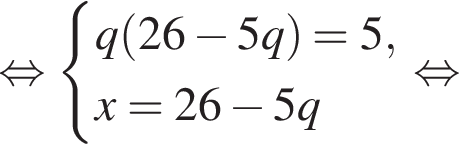
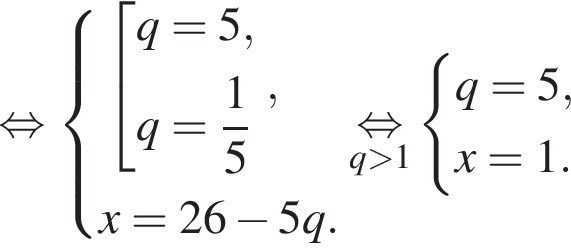
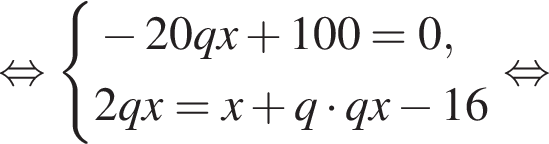
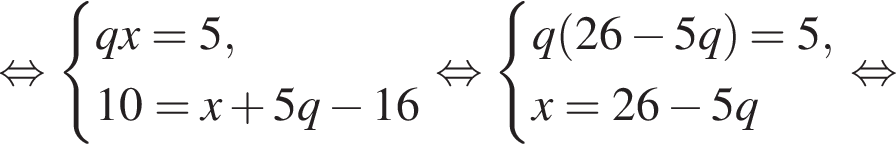
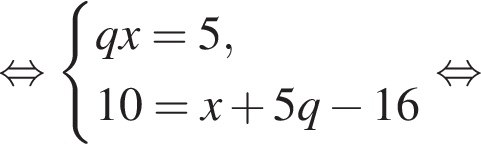
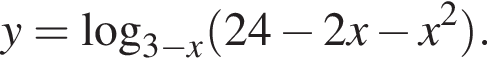
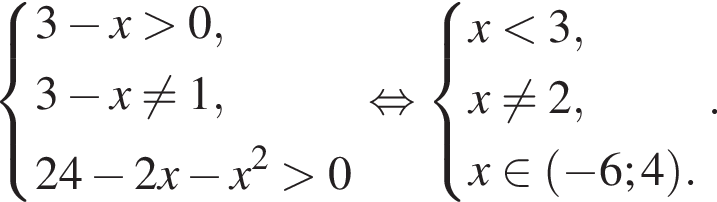
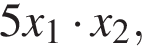 где
где 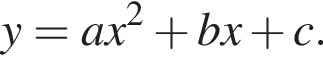 На рисунке изображена парабола с ветвями, направленными вниз, следовательно,
На рисунке изображена парабола с ветвями, направленными вниз, следовательно, 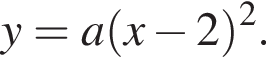 Для того, чтобы найти a, подставим в уравнение параболы точку (1;-1), через которую данная парабола проходит:
Для того, чтобы найти a, подставим в уравнение параболы точку (1;-1), через которую данная парабола проходит: 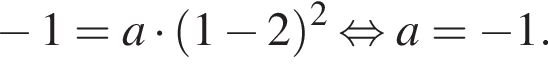 Таким образом, изображённая на графике парабола задается уравнением
Таким образом, изображённая на графике парабола задается уравнением 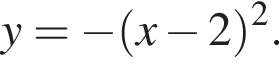
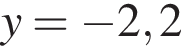 :
: 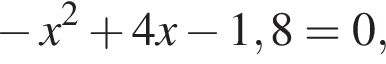 откуда по теореме Виета
откуда по теореме Виета 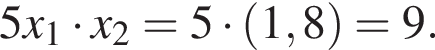
 Известно, что длины дуг пропорциональны посевным площадям. Пусть x — площадь, засеянная гречихой. Тогда
Известно, что длины дуг пропорциональны посевным площадям. Пусть x — площадь, засеянная гречихой. Тогда 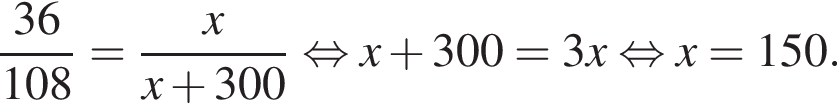
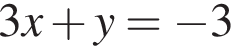 и
и 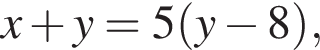 равна:
равна: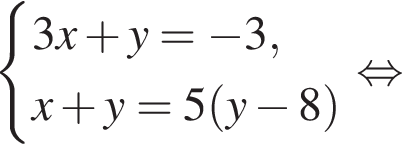
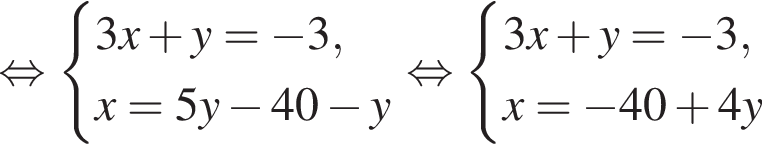
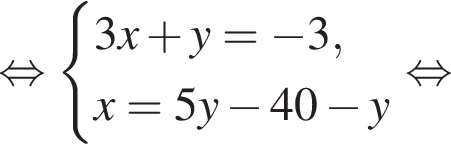
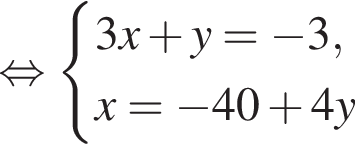
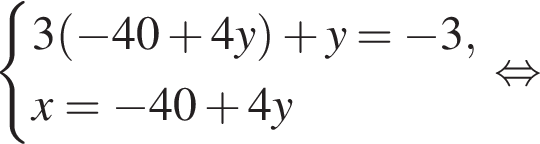
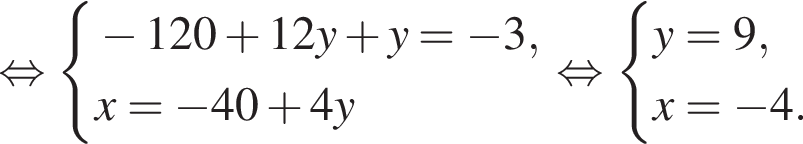
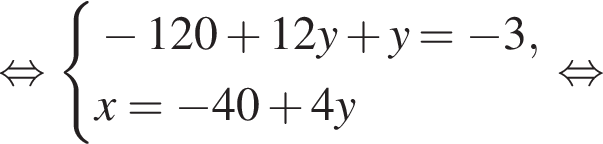
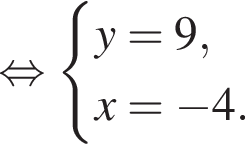
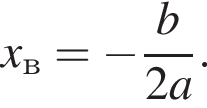 Поэтому
Поэтому 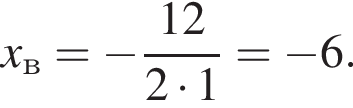 Поскольку y(xв) = −11, имеем:
Поскольку y(xв) = −11, имеем: